GRANDES MATEMÁTICOS QUE APORTARON AL TEMA DE LOS ANGULOS

Pitágoras de Samos

Nació : hacia el 569 a.C. en Samos, Jonia.

Murió : hacia el 475 a.C. en Metaponto (Lucania, Sur de Italia)

Filósofo y matemático griego nacido en la isla de Samos. Fue instruido en las enseñanzas de los filósofos jónicos, Tales de Mileto, Anaximandro y Anaxímenes. Posiblemente llegó a conocer a Tales, aunque no se sabe con certeza. Viajó por Babilonia y Egipto, y posiblemente también por la India. Durante estos viajes tuvo la oportunidad de conocer las matemáticas y la astronomía de estos pueblos, siendo influido también por las creencias de tipo religioso. Cuando regresa a Samos la isla está gobernada por el tirano Policrates. Su espiritu libre no acepta aquello y decide emigrar a Crotona, en la Magna Grecia, hoy sur de Italia (530 a. de C.). Allí funda una escuela o comunidad, considerada como algunos como una secta, con propósitos religiosos, políticos y filosóficos que alcanzó gran renombre y expansión. Su influencia política provocó levantamientos contra ellos, por lo que Pitágoras se vió obligado a huir a Tarento. Un año más tarde muere en Metaponto.

La comunidad pitagórica tenía unas creencias muy particulares, y se regía por unas normas muy estrictas. Una de sus doctrinas era la de la metempsicosis o transmigración de las almas, que consistía básicamente en que el alma era eterna y se reencarnaba en diferentes cuerpos a lo largo de sucesivas vidas hasta conseguir la perfecta purificación o catársis. Por este motivo tenían prohibido comer carne, ya que cualquier animal podía ser la reencarnación de un familiar o amigo fallecido. Desde el punto de vista moral, su objetivo era seguir el camino de la purificación que lleva a la catársis. Este fin se alcanzaría mediante el conocimiento de la filosofía y las matemáticas. Entre los alumnos de la escuela se distinguían los acusmáticos (oyentes) a los que les imponía silencio y una rigurosa disciplina de aprendizaje, y los matemáticos a los que se les permitía hacer preguntas y penetrar en las más profundas enseñanzas de la escuela. Un punto fundamental para entender la filosofía pitagórica es su conocido lema, que en palabras de Filolao dice así:

"Todas las cosas que pueden ser conocidas tienen número; pues no es posible que sin número nada pueda ser concebido ni conocido"

A partir de aquí, desarrollaron la teoría de que en el universo todo está armoniosamente ordenado (cosmos) y por lo tanto, puede ser explicado a través de las matemáticas. Fueron los primeros en entender la actividad matemática como una busqueda de la sabiduría, independiente de las necesidades de la vida práctica, y en plantearse la necesidad de estructurarla y discutir sus principios. En palabras de Proclo:

" ...transformó esta ciencia en una forma de educación liberal, examinando sus principios desde el comienzo y demostrando los teoremas de una forma inmaterial e intelectual"

Entre los avances realizados por los pitagóricos en el campo de las matemáticas, cabe destacar la demostración del conocido y por siempre famoso teorema de Pitágoras, y el descubrimiento de los números irracionales.

El teorema de Pitágoras

Este teorema era conocido en China, Mesopotamia y Egipto, mucho antes de los tiempos de Pitágoras. Una de las demostraciones más antiguas es la siguiente. Partiendo de un triángulo rectángulo como el de la figura 1 y utilizando cuatro de ellos, construimos la figura 2.

Figura 1

Figura 2

En la figura 2, el área del cuadrado grande es (a+b)². Pero la figura 2 se descompone en 4 triángulos y un cuadrado más pegueño. El área que obtenemos sumando las cinco partes es c²+4(ab/2) = c²+2ab. De aquí obtenemos que (a+b)² = c²+2ab; es decir, a²+2ab+b² = c²+2ab, y simplificando a²+b² = c². (q.e.d.)

Los egipcios lo utilizaron de una forma práctica para la construcción de ángulos rectos, hecho de gran utilidad a la hora de realizar obras arquitectónicas. Tomando una cuerda y haciéndole una serie de nudos de forma que queden determinada en ella 12 partes iguales, se ponía la cuerda formando un triangulo cuyos lados fuesen 3, 4 y 5 partes. El ángulo opuesto al lado mayor es siempre un ángulo de 90º.

Más mérito tiene todavía uno de los pueblos que vivía en Mesopotamia, los babilonios. Su método de escritura se conoce con el nombre de cuneiforme. Consistía en la grabación de una serie de marcas sobre tablillas de arcilla. Una de estas tablillas llamada Plimpton 322 fue descifrada en el siglo XIX, y lo que se encontró en ella fue una lista de ternas pitagóricas. Estas ternas consisten en conjuntos de tres números enteros que se corresponden con los tres lados de un triágulo rectangulo (verifican el teorema de Pitágoras). Algunos ejemplos de esto son: (3,4,5), (5,12,13), (6,8,10), (7,24,25), (12,16,20)...

Plimpton 322

Existe una cantidad muy numerosa de demostraciones del teorema de Pitágoras, pero quizás la más famosa es la que aparece en "Los Elementos" de Euclides. La idea es dividir el cuadrado mayor en dos partes de forma que cada parte sea igual al área de uno de los cuadrados pequeños. Demostraremos primero que el área del rectangulo amarillo (A'A''BM) es igual al área del cuadrado amarillo (ABPQ). Comencemos viendo que los triángulos ABM y CBP son congruentes (iguales). Esto es cierto porque:

a) Los ángulos obtusos de ABM y CBP son iguales.
b) El lado AB de ABM es igual al lado BP de CBP
c) El lado BM de ABM es igual al lado CB de CBP

Es decir, los triángulos tienen dos lados iguales e igual el ángulo comprendido.

Ahora bien, el triángulo ABM tiene un área igual a la mitad de la del rectángulo amarillo (A'A''BM) porque tienen la misma base y altura (para verlo tomar BM como base). Asimismo, el área del triángulo CBP es la mitad de la del cuadrado amarillo (ABPQ) por la misma razón (tomar BP como base). Como los dos triángulos son iguales, el rectángulo y el cuadrado también lo son. De forma análoga se procede con el rectángulo y el cuadrado de la izquierda y el teorema queda demostrado.

http://mimosa.pntic.mec.es/jgomez53/matema/conocer/pitagoras.htm.

THALES DE MILETO: 

THALES DE MILETO (624 a.C – 546 a.C.)

Nació y murió en la ciudad de Mileto. Sus padres fueron Examyes y Cleobuline. Fue maestro de Anaximandro. Ninguno de sus escritos sobrevivieron , por lo que es difícil saber exactamente cuáles fueron sus descubrimientos matemáticos. Probablemente se le atribuyan descubrimientos que no le corresponden. Lo que sabemos de Thales proviene de Aristóteles. Primero fue a Egipto y desde allí introdujo en Grecia Los estudios sobre Geometría.

La opinión antigua es unánime al considerar a Thales como un hombre excepcionalmente inteligente y como el primer filósofo griego, científico y matemático, pero actuaba como un ingeniero. Es considerado el primero de los Siete Sabios Griegos24. El hecho concreto que más aseguró su reputación fue la predicción de un eclipse de sol. en 585 a.C., que tuvo lugar exactamente el. 28 de mayo del año que él había predicho. Igualmente fue el primero en mantener que la luna brilla por el reflejo del sol.  

Según Proclo, primero fue a Egipto donde entró en contacto con la Geometría que luego introdujo a Grecia. 

Tomó prestada La Geometría de los egipcios y dio en ella un avance fundamental ya que fue el primero en emprender la tarea de demostrar exposiciones matemáticas mediante series regulares de argumentos. En otras palabras, inventó la matemática deductiva. Se le asignan entre otros los siguientes teoremas:  

1. Un ángulo inscripto en una semicircunferencia es un ángulo recto.

2. Todo círculo queda dividido en dos partes iguales por un diámetro.

3. Los ángulos básicos en un triángulo isósceles son iguales.

4. Los ángulos opuestos por el vértice que se forman al cortarse dos rectas, son iguales.

5. Si dos triángulos son tales que dos ángulos y un lado de uno de ellos son respectivamente iguales a dos ángulos y un lado del otro, entonces los dos triángulos son iguales.  

Midió la altura de las pirámides midiendo la altura de sus sombras en el momento en el cual la sombra de una persona es igual a su altura. Este razonamiento no parece surgir de conocimientos geométricos sino más bien de una observación empírica. Creyó que en el. momento en que la sombra de un objeto coincide con su altura, también eso es válido para cualquier objeto, por ejemplo, la pirámide.  

Luego utilizó conceptos similares al de la semejanza de triángulos. También calculó la distancia a un barco en el mar, para lo cual habría utilizado el teorema 3.

A continuación se muestra la demostración que aparece en la Proposición 32 del Libro III de Los Elementos de Euclides del teorema 1:

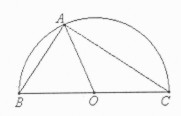
Como OA y OB son iguales, Los ángulos ABO y BOA también son iguales y como OA y OC son iguales, tos ángulos OAC y OCA son iguales. Por tanto, BAC es la suma de ABC y ACB, teniendo en cuenta que la suma de los tres ángulos de un triángulo BAC debe ser recto.

Creía que La Tierra era un disco plano que flotaba sobre agua y que todas La cosas .venian del agua. Explicaba los terremotos por el hecho de que la Tierra flote sobre agua. Fue el primero en tratar de explicar estos fenómenos en forma racional y no por medios sobrenaturales.

Hay dos anécdotas vinculadas a Thales. Una La cuenta Aristóteles, y dice que Thales usaba sus habilidades para deducir que La cosecha de aceitunas de La siguiente temporada sería muy buena. Entonces compraba todas las prensas de aceitunas, con Lo cual podía hacer fortunas cuando la abundante cosecha llegaba.  

Platón cuenta la otra anécdota: una noche Thales estaba observando el cielo y tropezó. Una sirviente lo Levantó y Le dijo: cómo pretendes entender lo que pasa en el cielo, si no puedes ver lo que está a tus pies.  

Es difícil escribir sobre Thales, como sobre otros personajes de esa época, porque era común acreditarles a hombres famosos descubrimientos que no hicieron. Por ejemplo, no hay constancia histórica de que Thales haya enunciado eL teorema que conocemos como Teorema de Thales, aunque si es cierto que Thales trabajó sobre la proporcionalidad de segmentos al calcular alturas midiendo las sombras.

En el momento de morir pronunció Las siguientes palabras: «Te alabo, ¡oh Zeus!, porque me acercas a ti. Por haber envejecido, no podía ya ver las estrellas desde la tierra. » 

http://historiaybiografias.com/matematico1/

ERATOSTENES

Eratóstenes (c. 284-c.- 192 a.C.), matemático, astrónomo, geógrafo, filósofo y poeta griego. Fue el primero que midió con buena exactitud el meridiano terrestre. Para ello ideó un sistema a partir de la semejanza de triángulos. Erastótenes midió en primer lugar la distancia entre dos ciudades egipcias que se encuentran en el mismo meridiano: Siene (Assuán) y Alejandría.

Esto lo hizo a partir del tiempo que tardaban los camellos en ir de una ciudad a otra.

Después se dio cuenta que el día del solsticio de verano a las 12 del mediodía el Sol alumbraba el fondo de un pozo muy profundo en la ciudad de Siene y que a esa misma hora el sol proyectaba una sombra en Alejandría. A raíz de esta circunstancia determinó, calculando el radio de la Tierra, que la longitud del meridiano debía ser 50 veces mayor que la distancia entre las ciudades. El resultado que obtuvo Erastótenes para el meridiano, en medidas modernas, viene a ser 46.250 km., cifra que excede a la medida real sólo en un 16%. Eratóstenes también midió la oblicuidad de la eclíptica (la inclinación del eje terrestre) con un error de sólo 7' de arco, y creó un catálogo (actualmente perdido) de 675 estrellas fijas. Su obra más importante fue un tratado de geografía general. Tras quedarse ciego, murió en Alejandría por inanición voluntaria.

ADAPTACIÓN DE LO QUE HIZO ERATÓSTENES

Eratóstenes, bibliotecario de la biblioteca de Alejandría, sospechaba que la Tierra era esférica.
Allí encontró un libro en el que decía que en la ciudad egipcia de Syene, el día 22 de Junio al mediodía, se veía el fondo de un pozo profundo. Con este dato confirmó sus sospechas: la Tierra era esférica y se propuso medir la circunferencia de esta. Él midió el ángulo de inclinación de los rayos do sol en Alejandría el día 22 de junio al mediodía, el resultado del ángulo fue de 7,2º.

Decidió medir la distancia entre Syene y Alejandría. Para esto usó el tiempo que le llevaba a las caravanas de camellos hacer el recorrido.
Otras versiones sostienen que contrató a un hombre para que hiciese el camino contando los pasos.

Alejandría y Syene se encuentran, aproximadamente, en el mismo meridiano terrestre. Cuando el Sol pasa por el meridiano, en el mediodía solar, Alejandría, Syene, el sol y el centro de la Tierra se encuentran en el mismo plano.

El resultado fue de 39 690 Km, cometiendo un error de un –0.1% , con respecto al valor real.

http://enebro.pntic.mec.es/~jhep0004/Paginas/ElenManu/ERATOSTENES.htm

EUCLIDES

Euclides es, sin lugar a dudas, el Matemático más famoso de la antigüedad y quizás el más nombrado y conocido de la historia de las Matemáticas.

Se conoce poco de la vida de Euclides, sin embargo, su obra sí es ampliamente conocida. Todo lo que sabemos de su vida nos ha llegado a través de los comentarios de un historiador griego llamado Proclo. Sabemos que vivió en Alejandría (Egipto), al parecer en torno al año 300 a.c. Allí fundó una escuela de estudios matemáticos. Por otra parte también se dice que estudió en la escuela fundada por Platón.

Su obra más importante es un tratado de geometría que recibe el título de "Los Elementos", cuyo contenido se ha estado (y aún se sigue de alguna manera) enseñando hasta el siglo XVIII, cuando aparecen las geometrías no euclídeas.
 

"LOS ELEMENTOS":
"Los Elementos" ha tenido más de 1.000 ediciones desde su primera publicación en imprenta en 1482. Se puede afirmar, por tanto, que Euclides es el matemático más leído de la historia.

Esta obra es importante, no tanto por la originalidad de sus contenidos, sino por la sistematización, el orden y la argumentación con la que está constituida. Euclides recopila, ordena y argumenta los conocimientos geométrico-matemáticos de su época, que ya eran muchos.

Euclides construye su argumentación basándose en un conjunto de axiomas (principios o propiedades que se admiten como ciertas por ser evidentes y a partir de los cuales se deduce todo lo demás) que Euclides llamó postulados. Los famosos cinco postulados de Euclides, que ofrecemos a continuación, son:
I.- Dados dos puntos se pueden trazar una recta que los une.

II.- Cualquier segmento puede ser prolongado de forma continua en una recta ilimitada en la misma dirección.

III.- Se puede trazar una circunferencia de centro en cualquier punto y radio cualquiera.
 IV.- Todos los ángulos rectos son iguales.
 
V.- Si una recta, al cortar a otras dos, forma los ángulos internos de un mismo lado menores que dos rectos, esas dos rectas prolongadas indefinidamente se cortan del lado en el que están los ángulos menores que dos rectos.

Este axioma es conocido con el nombre de axioma de las paralelas y también se enunció más tarde así:

 V.- Por un punto exterior a una recta se puede trazar una única paralela.
Este axioma, que al parecer no satisfacía al propio Euclides, ha sido el más controvertido y dio pie en los siglos XVIII y XIX al nacimiento de las geometría no-Euclídeas.
"Los Elementos" es una verdadera reflexión teórica de y sobre matemáticas. En la práctica totalidad de su obra, que consta de 465 proposiciones, 93 problemas y 372 teoremas, ¡no aparecen números! Euclides, además, escribió sobre música y óptica, tiene una obra titulada "Sofismas" que, dice Proclo, sirvepara ejercitar la inteligencia.
Para acabar podemos citar un par de anécdotas que nos ilustrarán, aún más, sobre la vida y gestos de Euclides:
En una ocasión, el rey Ptolomeo preguntó a Euclides si había un camino más breve que el que él utilizaba en "Los Elementos" para estudiar Geometría, él respondió que no existen caminos "reales" en la geometría.Con este juego de palabras, Euclides le vino a decir al rey que no existen privilegios en la geometría.
En otra ocasión, uno de sus estudiantes preguntó a Euclides qué ganaba con lo que había aprendido de la geometría: El maestro ordenó a su esclavo que le entregase una moneda (óbolo) a aquel estudiante, para que "ganara" algo con lo que aprendía de geometría, dando a entender que aquel muchacho no había entendido nada de la grandeza de la geometría y de lo desinteresado de ésta.

OTRAS IMÁGENES SOBRE EUCLIDES

 

Imagen de Euclides en una litografía de Fiorini, extraída del Diccionario de Autores.


 



 

            

Una imagen de Euclides sobre una página de Los Elementos. Extraída de la Historia de pensamiento.

 

 

Primera página de Los Elementos, en la primera edición impresa en latín en 1492, con traducción de Campanus. Imagen extraída del servidor de internet de la Universidad de St Andrews en Escocia.







 

                     









http://enebro.pntic.mec.es/~jhep0004/Paginas/ElenManu/euclides.htm